This post is a quick look at the new preprint of a paper called Efficient and Robust Search of Microbial Genomes via Phylogenetic Compression by Břinda et al.

The idea of the paper is to compress large collections of bacterial genomes with methods that are informed by phylogeny. The authors claim they can achieve orders of magnitude smaller space than regular gzip. Let’s investigate.

How does it work

The authors have a generic compression pipeline that first builds a phylogenetic tree of the input genomes, and then uses this to organize the data into a more compressible form before feeding it to a general-purpose compressor such as XZ. They demonstrate this approach on three different types of data:

1. Reference genomes
2. K-mer sets of reference genomes
3. Bit-sliced bloom filters (BIGSI) of k-mer sets of reference genomes

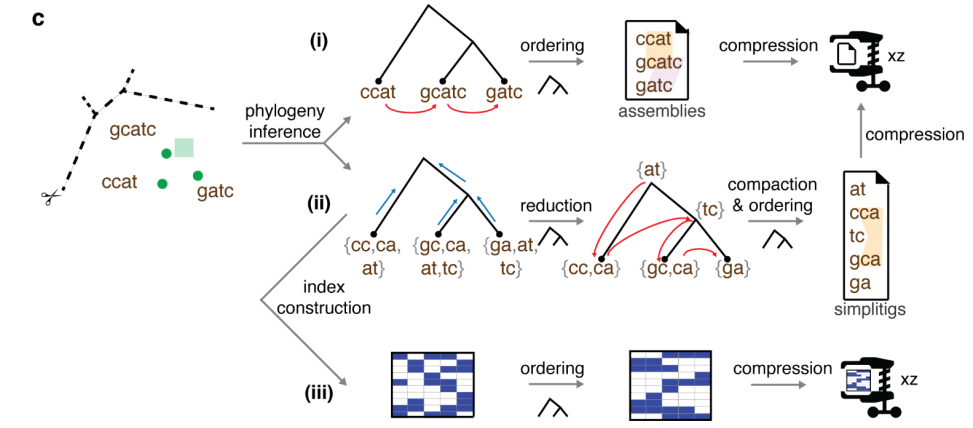
The tree helps compressing these three types of data as follows:

1. In case of reference genomes, the authors simply concatenate the reference genomes in left-to-right order in the tree, and give the concatenation to the XZ compressor. This works well because XZ is based on a dictionary compression algorithm which scans the input, encoding new text by combining phrases recently seen in the input. When similar genomes are nearby, XZ is able the encode the next genome by piecing together phrases from the nearby genomes.
2. In case of k-mer sets, the k-mers of each genome are inserted into the leaf corresponding to that genome. The same k-mer may occur in many leaves, so they compress the data by pushing k-mers up the tree to common ancestors. If there is an internal node X such that all leaves under X contain some common subset of k-mers, those k-mers are deleted from the leaves and added to X. The k-mers in each node are finally compressed by assembling them into spectrum preserving string sets using the Simplitig algorithm.
3. In the case of the bit-sliced bloom filters, the individual bloom filters are reordered left-to-right according to phylogeny. Since similar genomes have similar bloom filters, the XZ compressor benefits significantly from this reordering.

These methods make a lot of sense to me. The reordering of the genomes reminds me of Burrow-Wheeler-transform-based compression methods that reorder the characters of the input in a reversible fashion to cluster occurrences of the same characters together. But now, the reordering happens at the level of genomes, not individual characters. I’m still wondering how well their method compares to a run-length compressed Burrows-Wheeler transform. I’m also wondering how the k-mer compression method works compared to the Sparse Binary Relation Wavelet tree of Karasikov and others. Though I’m not sure if either of these two data structures are feasible to construct on datasets of this scale.

The authors here also provide a search algorithm. Let’s see how it works.

Searching

The paper proposes a way to align sequence reads against the compressed XZ-compressed database of microbial genomes. It works in two phases. First, the read is pseudoaligned (my word, not theirs) against bit-sliced k-mer-bloom-filters to find genomes that could potentially match with the query. Next, they decompress the parts of the input that have the potential matches, build a minimizer indexes for those parts (minimap2), and align against those (edit: apparently, they actually decompresss the whole data, see this Tweet by Břinda). The performance is as follows:

For example, they were able to align 191Mbp of M. tuberculosis reads in 4.29h using 8 cores and 26.2GB of RAM. The RAM usage is really impressive! These genomes take terabytes of space uncompressed. I’m not too excited by the speed however. That is only 12k nucleotides per second, so I would not exactly call this high-throughput bioinformatics.

I’m wondering which fraction of the total time was spent in the bloom filter index, the XZ decompression and the minimap2 indexing and alignment. For example, in the plasmid queries, I would expect there to be a huge number of hits to different species. Does the algorithm end up decompressing most of the database?

Conclusion

This was just a quick look at the paper. There is a lot more that I did not cover. I find this a very interesting piece of work and I’m surprised how well the databases compress with their approach. Congrats to the authors for this paper!